Dneuromodule | SuperCollider 3.12.2 Help

Description

The discrete time dynamics of a neural network can be described by initial state, bias, and the weights of the influence between the nodes. This demand rate ugen simulates the bahavior for any number of nodes.

The implementation follows the paper: Frank Pasemann, Complex dynamics and the structure of small neural networks, Network: Comput. Neural Syst. 13 (2002) p. 195–216.

In the core, Dneuromodule implements the following formula:

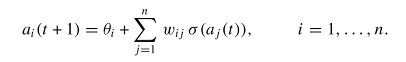
As transfer function (sigma) tanh is used.

Class Methods

Dneuromodule.new(numChannels, theta, x, weights)

Arguments:

numChannels	Number of nodes that represent cells, which is also the number of output channels of the UGen.
theta	Bias for each node. Should be an array on `numChannels` size. This argument is also the usual way to define an input into the node. It can contain demand rate ugens or any other ugens or numbers.
x	Initial value of each node. Should be an array on `numChannels` size.
weights	An `n x n` matrix of inter-node connections that represent synapses. Should be an array of `numChannels * numChannels` size. It can contain demand rate ugens or any other ugens or numbers.