Description
Performs waveshaping on the input signal by indexing into the table.
Class Methods
Shaper.ar(bufnum, in: 0.0, mul: 1.0, add: 0.0)
Shaper.kr(bufnum, in: 0.0, mul: 1.0, add: 0.0)
Arguments:
| bufnum |
The number of a buffer filled in wavetable format containing the transfer function. |
| in |
The input signal. |
Inherited class methods
Instance Methods
Inherited instance methods
Examples
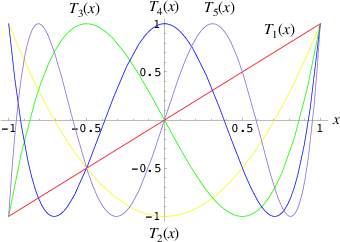
Wave shaping transfer functions are typically designed by using Chebyshev polynomials to control which harmonics are generated when a cosine wave is passed in. The implementation in SuperCollider compensates for the DC offset due to even polynomial terms, making sure that when 0 is put into the transfer function, you get 0 out. By default, normalization is set to true, which avoids output overload. If you want to construct a transfer function without this, you need to be careful with the final output scaling, since it could easily overload the -1 to 1 range for audio.
For those who like to make their own wavetables for arbitrary shapers, your buffer must be in wavetable format to have a valid transfer function. Wavetable format is a special representation to make linear interpolation faster (see at the bottom of this file). You don't have to worry about this directly, because there are two straight forward ways to get wavetables into a server buffer. First, the server can generate them (see the Buffer help file for the methods sine1, sine2, sine3 and cheby):
Or, you can calculate the transfer function in a client-side array (Signal class) then convert it to a wavetable and send the data over.
This way of working then allows you to get creative with your transfer functions!
link::Classes/Shaper::